Back to: Robotics & Artificial Intelligence (Class IX)

Role of Data
Data refers to any collection of information that has been organized in a structured or unstructured way. Data refers to any collection of facts, figures or information that can be processed, analyzed and interpreted to derive insights, knowledge and understanding. It can be in the form of numbers, text, images, audio, video or any other digital format.
Difference between Information and Data
| DATA | INFORMATION |
| Data are the variables that help to develop ideas/conclusions. | Information is meaningful data. |
| Data are text and numerical values. | Information is refined form of actual data. |
| Data doesn’t rely on Information. | While Information relies on Data. |
| Bits and Bytes are the measuring unit of data. | Information is measured in meaningful units like time, quantity, etc. |
| Data can be easily structured as the following: 1.Tabular data 2.Graph 3.Data tree | Information can also be structured as the following: 1. Language 2. Ideas 3. Thoughts |
| Data does not have any specific purpose | Information carries a meaning that has been assigned by interpreting data. |
| It is low-level knowledge. | It is the second level of knowledge. |
| Data does not directly helps in decision making. | Information directly helps in decision making. |
| Data is collection of facts, which it self have no meaning. | Information puts those facts into context. |
| Example of data is student test score. | Example of information is average score of class that is derived from given data. |
DIKW Model
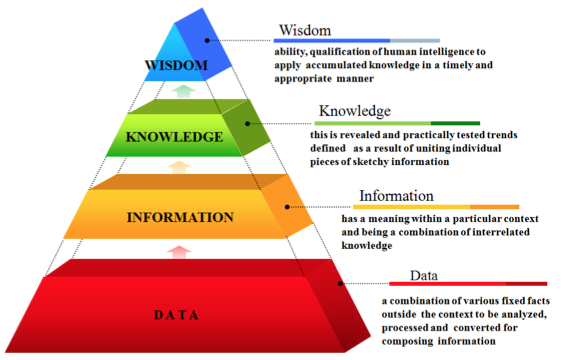
The data, information, knowledge, and wisdom (DIKW) model explains how IT service desk teams can generate knowledge based on their everyday activities. This also shows how the transformation of data into information, knowledge, and wisdom occurs along with the relationship between them. This model is also known as the DIKW pyramid or DIKW hierarchy.
Data
Data is the collection of discreet facts about events in the form of numbers, characters, and specific or relative values that the organization can gather. The key activities to be performed at this stage are:
- Identifying a reliable source to get data
- Archiving and deleting the appropriate data
Information
This stage is about adding context to data. The key activities to be performed in this stage are:
- Converting data into information while maintaining data integrity
- Managing information the right way by making it easy for end users to search and use.
Knowledge
Knowledge is derived from experience. It may involve expertise, values, and judgments of members of the IT service desk team such as the knowledge managers, subject matter experts, technicians, or end users. Knowledge created in this stage facilitates smart decision-making.
Wisdom
Wisdom is the culmination of data, information, and knowledge. It adds value to knowledge management. This value is created though dynamic planning, problem solving, strategic planning, and discernment.
Evolution of Computing
Binary Logic System
A Binary Logic System is the fundamental basis of digital computing, where all data and computations are represented using two states: 0 (off/false) and 1 (on/true). This system uses binary numbers and logical operations to perform calculations, make decisions, and control the behavior of digital circuits.
Key Concepts of Binary Logic System
- Binary Numbers:
- A binary number is a number expressed in the base-2 numeral system, which uses only two digits: 0 and 1.
- For example, the binary number 1011 represents the decimal number 11.
- Computers use binary numbers to represent all types of data, including text, images, and instructions.
- Logic Gates:
- Logic gates are the building blocks of a binary logic system. They perform basic logical functions using binary inputs (0 or 1) and produce a binary output. The most common logic gates are:
- AND Gate: Outputs 1 only if both inputs are 1.
- OR Gate: Outputs 1 if at least one input is 1.
- NOT Gate: Outputs the opposite of the input (1 becomes 0, and 0 becomes 1).
- NAND Gate: Outputs 0 only if both inputs are 1 (NOT of AND).
- NOR Gate: Outputs 1 only if both inputs are 0 (NOT of OR).
- XOR Gate (Exclusive OR): Outputs 1 if only one of the inputs is 1.
- XNOR Gate (Exclusive NOR): Outputs 1 if both inputs are the same.
Applications of Binary Logic System
- Computers and Processors: All operations in a computer’s central processing unit (CPU) are performed using binary logic. The CPU uses logic gates to perform arithmetic operations, make decisions, and execute instructions.
- Memory Devices: Memory devices, such as RAM and ROM, store and retrieve data in binary form. Each bit of memory represents a 0 or 1.
- Digital Communication: Binary logic is used in digital communication systems to encode, transmit, and decode data over networks.
- Digital Electronics: All modern digital electronics, including calculators, mobile phones, digital watches, and microcontrollers, operate using binary logic.
Why Binary Logic is Fundamental to Computing
- Simplicity and Reliability: Binary logic is simple to implement in hardware using transistors, which have two stable states: on and off. This makes digital circuits reliable and efficient.
- Error Detection and Correction: Binary data can easily be checked for errors and corrected using various coding techniques.
- Compatibility with Digital Devices: All digital devices, from microchips to complex supercomputers, use binary logic to process information.
Deterministic Problems and Deterministic Computing
Deterministic Computing– refers to a type of computation where the outcome is precisely determined by the initial state and inputs. In deterministic computing, given the same starting conditions and inputs, the system will always produce the same output. There is no randomness or uncertainty involved; every step of the computation is predictable and follows a specific algorithm or set of rules.
Key Features of Deterministic Computing:
- Predictable Results: Every operation is well-defined, and the output is always the same for a given set of inputs.
- Repeatability: Re-running the computation with the same inputs will always produce the same output.
- Fixed Rules: Computation follows a pre-determined algorithm or logic that does not change over time.
Deterministic Problems– are problems that have a clear, predictable outcome given a specific set of inputs and rules. These problems can be fully solved using deterministic algorithms that always produce the same result for the same inputs. Ex:
- Arithmetic Operations: Simple mathematical problems like addition, subtraction, multiplication, and division. For example, (2 + 2) will always equal 4.
- Sorting Algorithms: Sorting a list of numbers using a defined algorithm like QuickSort or MergeSort will always produce the same sorted list from the same input.
- Pathfinding in a Known Environment: Finding the shortest path between two points on a static, known map (like using Dijkstra’s algorithm) is deterministic because the environment does not change.
- Compiling Code: When a compiler processes source code into machine code, it follows a fixed set of rules and always produces the same output binary for the same input source code.
Limitations of Deterministic Computing in Solving Real-Life Problems
While deterministic computing is highly effective for solving problems with well-defined rules and inputs, it has significant limitations in dealing with many real-life situations that are inherently uncertain or variable.
Limitations:
- Cannot Handle Uncertainty: Real-world problems often involve uncertainties or incomplete information that deterministic algorithms cannot manage. For example, predicting stock market prices involves many unpredictable factors (economic changes, market sentiment, etc.).
- Lack of Flexibility: Deterministic systems are rigid; they cannot adapt to new or changing conditions. For instance, a robot using a deterministic algorithm may fail if it encounters an unexpected obstacle in its path.
- Not Suitable for Complex Systems: Many real-life problems are complex and involve numerous variables interacting in unpredictable ways, such as weather forecasting or human behavior analysis.
- Limited Problem Scope: Deterministic computing is only effective for problems where all variables are known and can be accurately measured or controlled.
Comparison Between Deterministic and Probabilistic Nature of Real-Life Problems
| Aspect | Deterministic Problems | Probabilistic (Real-Life) Problems |
|---|---|---|
| Definition | Problems with a known set of inputs and rules that always produce the same output. | Problems where outcomes are uncertain and involve randomness, incomplete data, or variability. |
| Predictability | Highly predictable; same input always leads to the same output. | Not always predictable; outcomes may vary even with similar inputs. |
| Examples | Simple math calculations, sorting algorithms, compiling code. | Weather forecasting, stock market prediction, medical diagnosis, and traffic management. |
| Nature of Solution | Fixed, follows a set of well-defined rules or algorithms. | Based on probability, statistics, and machine learning to handle uncertainty and variability. |
| Flexibility | Low flexibility; cannot adapt to new or changing inputs. | High flexibility; can adapt to new data or changes in the environment. |
| Adaptability | Limited; needs precise data and rules to operate effectively. | High; can handle uncertain or incomplete data, making it suitable for dynamic environments. |
| Application Scope | Suitable for simple, well-defined problems with clear rules. | Suitable for complex, uncertain, and dynamic problems. |
Illustrating the Limitations of Deterministic Computing with Examples
Weather Forecasting
- Deterministic Approach: Using a fixed mathematical model to predict the weather assumes perfect knowledge of all variables like temperature, pressure, and humidity. However, small changes in these variables can lead to vastly different outcomes (the “butterfly effect”), making deterministic models insufficient.
- Limitation: Weather systems are inherently chaotic and involve many interacting variables, which are difficult to measure precisely. A deterministic approach cannot handle the uncertainties involved in predicting the weather accurately.
Stock Market Prediction
- Deterministic Approach: A deterministic algorithm would require a complete understanding of all factors influencing stock prices, such as economic indicators, political events, and market psychology.
- Limitation: The stock market is influenced by unpredictable factors, like investor behavior, market sentiment, or sudden geopolitical events. A deterministic model cannot account for these random or unforeseen events.
Probabilistic Approaches to Real-Life Problems
In contrast to deterministic computing, probabilistic approaches use probability and statistical methods to handle uncertainty and make predictions in real-world scenarios. These methods allow for flexibility and adaptability when dealing with problems where exact outcomes cannot be guaranteed. Ex:
- Machine Learning: Algorithms like decision trees, neural networks, and Bayesian networks learn from data and make predictions or decisions even when the data is incomplete or noisy.
- Applications: Autonomous vehicles (adjusting to changing traffic conditions), spam email detection, personalized recommendations (such as on Netflix or Amazon), and medical diagnosis.
Logic Gate
AND Gate
2.4.1 AND gate
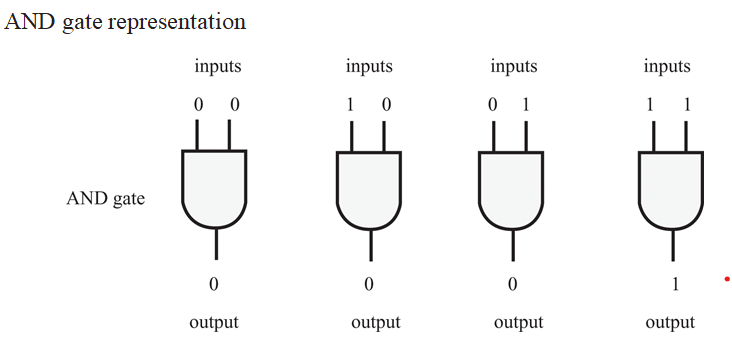
This gate acts in the same way as the logical operator ‘and’ works. An AND operation produces an output of logic-0 if at least one of the input is zero. Output will be logic-1 if all the inputs are logic-1. Truth table of AND operation is shown below. A truth table is a list of all possible combination of input logic levels along with corresponding output level.
Truth Table for AND operation
| Input | Output | |
| A | B | C = A.B |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
The equation for logic AND operation
C = AB
OR Gate
This operation is represented by plus (+) sign. The OR gate produces an output of logic-1 if at least one of the inputs is logic-1.
Truth Table for OR operation
| Input | Output | |
| A | B | C = A + B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Equation of OR operation:
C = A + B
Not Gate
The NOT operation represents complement or inverse of inputs. A prime or bar represents this operation. The truth table for NOT operation is given in Table.
Truth table for NOT operation
| (Input) | (Output) |
| A | A |
| 0 | 1 |
| 1 | 0 |

Equation for NOT operation
Q = A
- NOR operation is combination of OR and NOT. NAND operation is combination of AND and NOT.
NOR Gate
It is the NOT-OR gate. The output is true when neither A nor B is true. If any one of the input variables is true then output is false. NOR gate represents complement of the OR operation. The graphic symbol for the NOR gate consists of an OR symbol with a bubble on the output, denoting that a complement operation is performed on the output of the OR gate.
Truth table of NOR operation
| Input | Output | |
| A | B | |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
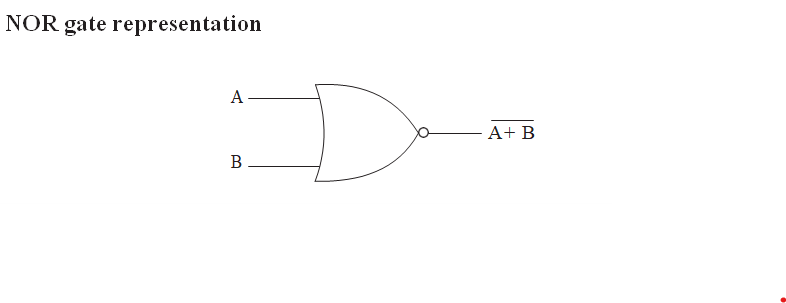
Equation for NOR gate

NAND Gate
The NAND gate represents the complement of the AND operation. The graphic symbol for the NAND gate consists of an AND symbol with a bubble on the output, denoting that a complement operation is performed on the output of the AND gate.
Truth table of NAND operation
| Input | Output | |
| A | B | |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
NAND gate representation

Equation for NAND gate

